Equação Do 2º Grau: Como Resolver, Exercícios – Mundo Educação. A matemática, muitas vezes vista como um universo árido de números e fórmulas, revela-se, na equação do segundo grau, um portal para um mundo de elegância e precisão. Nesta jornada, desvendaremos os segredos por trás dessa equação aparentemente complexa, explorando seus conceitos fundamentais, métodos de resolução e aplicações práticas.
Prepare-se para desvendar a beleza intrínseca da matemática e dominar uma ferramenta poderosa que abre portas para diversas áreas do conhecimento. A aventura começa agora!
Vamos mergulhar no fascinante mundo das equações do segundo grau! Começaremos definindo a forma geral da equação (ax² + bx + c = 0), entendendo o significado de cada coeficiente (a, b, c) e a importância do discriminante (Δ) para determinar a natureza das raízes. Exploraremos dois métodos principais de resolução: a consagrada fórmula de Bhaskara, com seus passos meticulosamente explicados, e o método de fatoração, ideal para equações mais simples.
Compararemos as vantagens e desvantagens de cada técnica, guiando você na escolha do método mais eficiente para cada situação. Além disso, apresentaremos aplicações práticas em física e geometria, solidificando seu aprendizado com exercícios resolvidos e propostos, de diferentes níveis de dificuldade. Prepare-se para dominar as equações do segundo grau e expandir seus horizontes matemáticos!
Conceitos Fundamentais da Equação do 2º Grau: Equação Do 2º Grau: Como Resolver, Exercícios – Mundo Educação
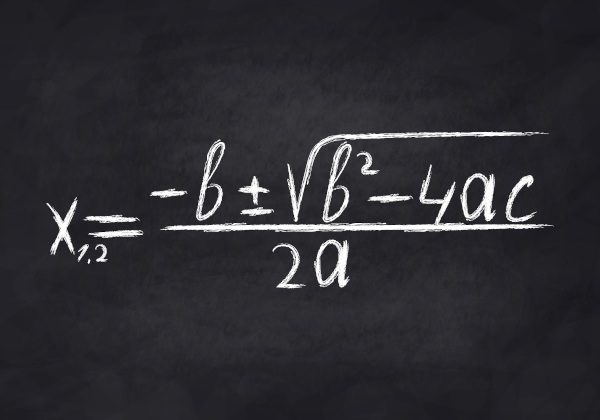
Embarque conosco numa jornada fascinante pelo mundo das equações do segundo grau! Prepare-se para desvendar os mistérios por trás dessas expressões matemáticas, que, apesar de sua aparente complexidade, revelam uma elegância e uma lógica surpreendentes. Dominar esses conceitos abrirá portas para a compreensão de inúmeros fenômenos, desde o lançamento de projéteis até o desenho de curvas em arquitetura.
A equação do 2º grau é uma ferramenta poderosa, capaz de modelar uma vasta gama de situações reais. Sua beleza reside na capacidade de descrever, com precisão, a trajetória de um objeto em queda livre, a forma de uma parábola em um gráfico ou mesmo o crescimento populacional de uma colônia de bactérias. Vamos desvendar seus segredos.
Forma Geral da Equação do 2º Grau e seus Componentes, Equação Do 2º Grau: Como Resolver, Exercícios – Mundo Educação

A forma geral de uma equação do segundo grau é representada por
ax² + bx + c = 0
, onde ‘a’, ‘b’ e ‘c’ são coeficientes numéricos, sendo ‘a’ diferente de zero (a ≠ 0). ‘a’ determina a concavidade da parábola (se abre para cima ou para baixo), ‘b’ influencia o posicionamento do vértice da parábola e ‘c’ representa o ponto onde a parábola intercepta o eixo y. Observe que ‘a’, ‘b’ e ‘c’ podem assumir valores positivos, negativos ou zero, exceto ‘a’, que obrigatoriamente precisa ser diferente de zero para que a equação seja de segundo grau.
O Significado do Discriminante (Δ) e a Natureza das Raízes

O discriminante (Δ), calculado pela fórmula
Δ = b²-4ac
, é um elemento crucial na resolução de equações do segundo grau. Ele determina o número e a natureza das raízes (ou soluções) da equação. Se Δ > 0, a equação possui duas raízes reais e distintas. Se Δ = 0, a equação possui duas raízes reais e iguais (uma raiz dupla). Se Δ < 0, a equação não possui raízes reais, mas sim duas raízes complexas conjugadas.
Cálculo do Discriminante (Δ) e das Raízes da Equação

O cálculo do discriminante é simples e direto, bastando substituir os valores de ‘a’, ‘b’ e ‘c’ na fórmula Δ = b²
4ac. Uma vez calculado o discriminante, podemos determinar a natureza das raízes. Para encontrar as próprias raízes, utilizamos a fórmula de Bhaskara
x = (-b ± √Δ) / 2a
Esta fórmula nos fornece as duas raízes (x 1 e x 2) da equação. Note o sinal ±, indicando que devemos calcular duas soluções: uma utilizando o sinal de ‘+’ e outra utilizando o sinal de ‘-‘.
Comparação entre os Métodos de Bhaskara e Fatoração

A resolução de equações do 2º grau pode ser feita por diferentes métodos, cada um com suas vantagens e desvantagens. A seguir, uma comparação entre a fórmula de Bhaskara e a fatoração:
| Método | Fórmula/Processo | Exemplo | Observações |
|---|---|---|---|
| Bhaskara | x = (-b ± √(b²
|
Para a equação x²
|
Sempre funciona, mesmo para equações com raízes não inteiras. |
| Fatoração | Encontrar dois números que somados resultem em ‘b’ e multiplicados resultem em ‘ac’. | Para a equação x²5x + 6 = 0, procuramos dois números que somados dão -5 e multiplicados dão 6. Esses números são -2 e -3. Portanto, (x – 2)(x – 3) = 0, resultando em x1 = 2 e x 2 = 3. | Funcional apenas para equações com raízes inteiras e facilmente fatoráveis. |

