Exemplos De Aplicação Do Teorema De Pitagoras – O Teorema de Pitágoras, um pilar da geometria, transcende os confins da teoria abstrata, encontrando aplicações práticas em uma ampla gama de campos. Desde a medição de alturas imponentes até o cálculo de distâncias inacessíveis, este teorema versátil desempenha um papel crucial em nossas vidas diárias.
Este artigo explorará as diversas aplicações do Teorema de Pitágoras, demonstrando sua relevância em engenharia, arquitetura e resolução de problemas cotidianos. Além disso, forneceremos uma tabela de referência prática e uma lista de perguntas frequentes para aprimorar ainda mais sua compreensão.
Exemplos Práticos do Teorema de Pitágoras
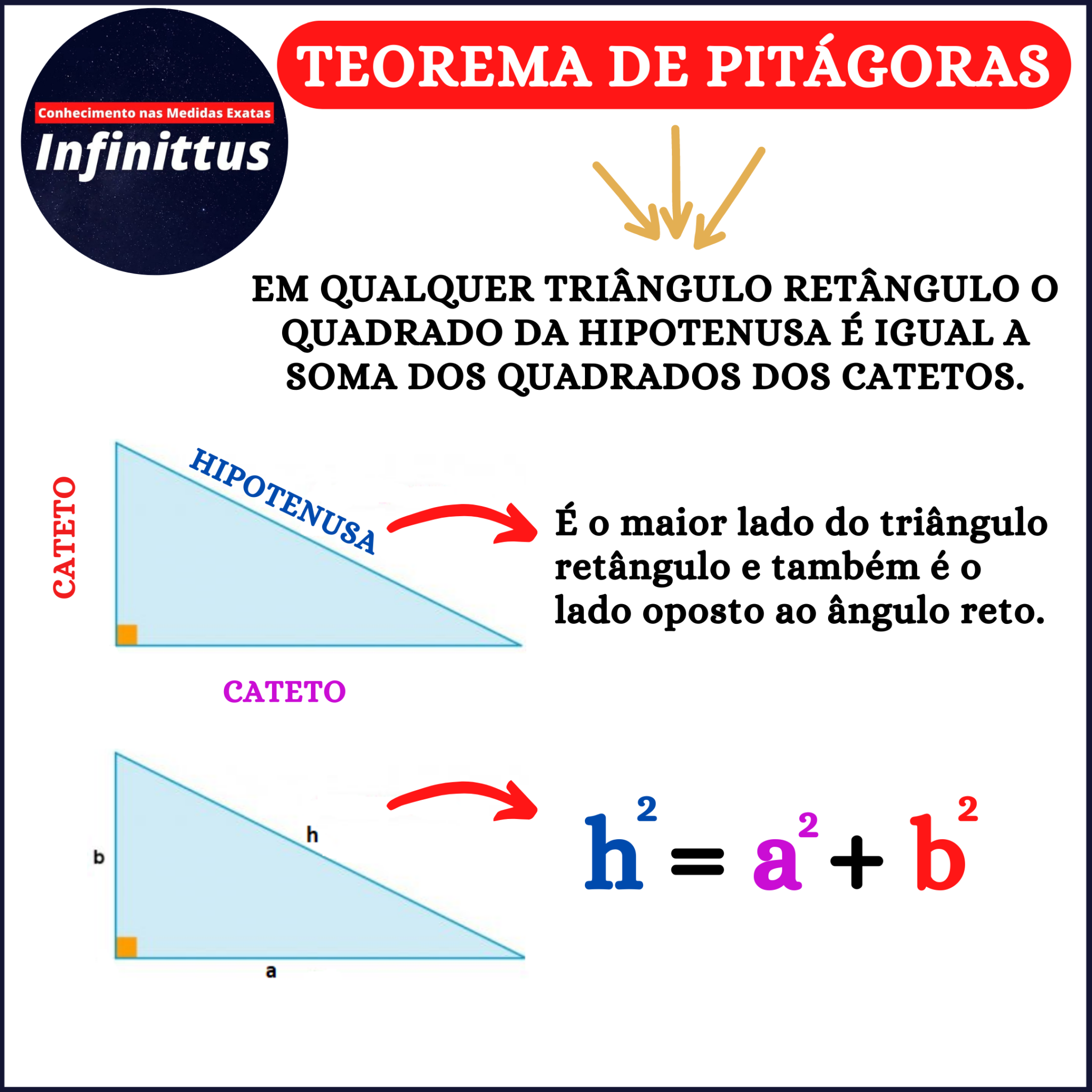
O Teorema de Pitágoras é uma ferramenta valiosa com diversas aplicações práticas em vários campos. Desde medir a altura de edifícios até calcular distâncias entre pontos, o teorema oferece uma solução eficiente para resolver problemas que envolvem triângulos retângulos.
Aplicações na Arquitetura
Na arquitetura, o Teorema de Pitágoras é usado para determinar a altura de edifícios ou outras estruturas. Medindo o comprimento da base do edifício e o ângulo de elevação do topo, é possível calcular a altura usando a fórmula do teorema: altura² = comprimento da base² + comprimento da hipotenusa².
Aplicações em Topografia
Em topografia, o teorema é usado para medir distâncias entre pontos inacessíveis. Por exemplo, para medir a distância entre dois pontos em lados opostos de um rio, os topógrafos medem a distância entre dois pontos acessíveis em uma margem do rio e os ângulos entre esses pontos e o ponto inacessível na outra margem.
Usando o Teorema de Pitágoras, eles podem calcular a distância entre os pontos inacessíveis.
Aplicações na Engenharia, Exemplos De Aplicação Do Teorema De Pitagoras
Na engenharia, o teorema é usado para calcular comprimentos de vigas, cabos e outros elementos estruturais. Por exemplo, para determinar o comprimento de uma viga que se estende diagonalmente entre dois pontos, os engenheiros usam o Teorema de Pitágoras para calcular o comprimento da hipotenusa do triângulo retângulo formado pela viga e as distâncias horizontais e verticais entre os pontos.
Aplicações na Física
Na física, o Teorema de Pitágoras é usado para calcular a velocidade de objetos em movimento. Por exemplo, para calcular a velocidade de um projétil lançado em um ângulo, os físicos usam o teorema para determinar a distância horizontal percorrida e a distância vertical alcançada.
A velocidade é então calculada dividindo a distância horizontal pelo tempo de voo.
Demonstrações Geométicas do Teorema de Pitágoras
O Teorema de Pitágoras é um importante teorema geométrico que estabelece uma relação entre os comprimentos dos lados de um triângulo retângulo. Uma demonstração geométrica é uma prova que usa figuras e diagramas para demonstrar um teorema.
Existem várias demonstrações geométricas do Teorema de Pitágoras, cada uma com sua abordagem única. Duas demonstrações clássicas são a Prova de Euclides e a Prova de Pitágoras.
Prova de Euclides
A Prova de Euclides é uma das demonstrações mais conhecidas do Teorema de Pitágoras. Ela usa um quadrado construído sobre a hipotenusa do triângulo retângulo e quatro triângulos retângulos menores construídos dentro do quadrado.
- Construa um quadrado sobre a hipotenusa do triângulo retângulo.
- Divida o quadrado em quatro triângulos retângulos menores.
- Observe que a área do quadrado é igual à soma das áreas dos quatro triângulos menores.
- A área do quadrado é (hipotenusa)².
- A área de cada triângulo menor é (cateto)²/2.
- Portanto, a área do quadrado é (hipotenusa)² = 2(cateto)² + 2(cateto)².
- Simplificando, obtemos o Teorema de Pitágoras: (hipotenusa)² = (cateto)² + (cateto)².
Prova de Pitágoras
A Prova de Pitágoras é outra demonstração clássica do Teorema de Pitágoras. Ela usa um triângulo retângulo com dois quadrados construídos sobre os catetos.
- Construa um triângulo retângulo.
- Construa um quadrado sobre cada cateto.
- Observe que a área do quadrado maior é igual à soma das áreas dos dois quadrados menores e da área do triângulo retângulo.
- A área do quadrado maior é (hipotenusa)².
- A área de cada quadrado menor é (cateto)².
- A área do triângulo retângulo é (cateto₁)(cateto₂)/2.
- Portanto, a área do quadrado maior é (hipotenusa)² = (cateto₁)² + (cateto₂)² + (cateto₁)(cateto₂)/2.
- Simplificando, obtemos o Teorema de Pitágoras: (hipotenusa)² = (cateto)² + (cateto)².
As demonstrações geométricas do Teorema de Pitágoras são baseadas nos princípios da geometria e fornecem uma compreensão visual e intuitiva do teorema. Elas têm implicações importantes na geometria, como a relação entre os lados de triângulos retângulos e o cálculo de distâncias e áreas.
Aplicações do Teorema em Engenharia e Arquitetura

O Teorema de Pitágoras é amplamente utilizado em engenharia e arquitetura para calcular comprimentos, áreas e volumes. Na engenharia, o teorema é empregado em projetos estruturais, determinando as dimensões de vigas, colunas e outras componentes. Na arquitetura, é aplicado na concepção de edifícios, ajudando a calcular as dimensões de salas, telhados e outros elementos estruturais.
Cálculo de Comprimentos
O teorema de Pitágoras é usado para calcular o comprimento de elementos estruturais, como vigas e colunas. Por exemplo, para determinar o comprimento da diagonal de uma viga retangular com largura de 10 cm e altura de 8 cm, podemos usar a fórmula:“`Diagonal² = Largura² + Altura²Diagonal² = 10² + 8²Diagonal² = 100 + 64Diagonal² = 164Diagonal = √164Diagonal = 12,8 cm“`
Cálculo de Áreas
O teorema de Pitágoras também é aplicado no cálculo de áreas de figuras geométricas, como triângulos e trapézios. Por exemplo, para calcular a área de um triângulo retângulo com catetos de 6 cm e 8 cm, podemos usar a fórmula:“`Área = (Base x Altura) / 2Área = (6 x 8) / 2Área = 24 cm²“`
Cálculo de Volumes
O teorema de Pitágoras é utilizado para calcular volumes de sólidos, como prismas e pirâmides. Por exemplo, para calcular o volume de um prisma retangular com comprimento de 10 cm, largura de 8 cm e altura de 6 cm, podemos usar a fórmula:“`Volume = Comprimento x Largura x AlturaVolume = 10 x 8 x 6Volume = 480 cm³“`
Vantagens e Limitações
O Teorema de Pitágoras é uma ferramenta valiosa em engenharia e arquitetura devido à sua simplicidade e precisão. No entanto, existem algumas limitações:*
-*Aplicabilidade a figuras planas
O teorema se aplica apenas a figuras planas, como triângulos e quadrados.
-
-*Erros de medição
Erros nas medições podem afetar a precisão dos cálculos.
-*Casos complexos
Para estruturas complexas, pode ser necessário utilizar métodos geométricos mais avançados.
Apesar dessas limitações, o Teorema de Pitágoras continua sendo uma ferramenta fundamental em engenharia e arquitetura, fornecendo soluções precisas para uma ampla gama de problemas de dimensionamento e cálculo.
Resolução de Problemas com o Teorema de Pitágoras
O Teorema de Pitágoras é uma ferramenta valiosa para resolver uma ampla gama de problemas envolvendo triângulos retângulos. Aqui está uma lista de problemas de amostra que podem ser resolvidos usando o teorema:
- Encontrar o comprimento da hipotenusa de um triângulo retângulo dados os comprimentos dos catetos.
- Encontrar o comprimento de um cateto de um triângulo retângulo dados os comprimentos da hipotenusa e do outro cateto.
- Determinar se um triângulo é retângulo dados os comprimentos dos seus lados.
- Resolver problemas de altura, distância e área envolvendo triângulos retângulos.
Para resolver esses problemas, siga estas instruções passo a passo:
- Identifique os lados conhecidos e desconhecidos do triângulo retângulo.
- Lembre-se que, em um triângulo retângulo, o quadrado do comprimento da hipotenusa é igual à soma dos quadrados dos comprimentos dos catetos.
- Substitua os valores conhecidos na fórmula do Teorema de Pitágoras e resolva para o lado desconhecido.
- Verifique se sua resposta faz sentido no contexto do problema.
Aqui estão alguns problemas específicos que podem ser resolvidos usando o Teorema de Pitágoras:
Problema 1:
Uma escada de 10 pés de comprimento encosta-se a uma parede. O pé da escada está a 6 pés da base da parede. Qual é a altura da parede que a escada alcança?
Problema 2:
Um terreno retangular tem um comprimento de 15 metros e uma largura de 8 metros. Qual é a distância diagonal de um canto do terreno ao canto oposto?
Problema 3:
Um triângulo tem lados com comprimentos de 5 cm, 12 cm e 13 cm. Esse triângulo é retângulo?
Tabela de Referência para o Teorema de Pitágoras: Exemplos De Aplicação Do Teorema De Pitagoras

O Teorema de Pitágoras é uma ferramenta fundamental para calcular comprimentos, áreas e volumes em diversas aplicações práticas. Uma tabela de referência com valores trigonométricos comuns (seno, cosseno, tangente) para ângulos selecionados pode simplificar significativamente esses cálculos.
Esta tabela fornece valores numéricos precisos para os seis ângulos mais comuns (0°, 30°, 45°, 60°, 90° e 180°), facilitando a determinação dos comprimentos dos lados de triângulos retângulos.
Valores Trigonométricos Comuns
| Ângulo (graus) | Seno | Cosseno | Tangente |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | ∞ |
| 180° | 0 | -1 | 0 |
O Teorema de Pitágoras é mais do que uma fórmula matemática; é uma ferramenta poderosa que nos permite navegar no mundo ao nosso redor. Seja medindo a altura de um arranha-céu ou calculando a área de um terreno, este teorema continua a ser um recurso inestimável para profissionais e curiosos.
Ao compreender as aplicações práticas do Teorema de Pitágoras, podemos apreciar sua versatilidade e relevância no mundo real. Que este artigo sirva como um guia para explorar as muitas maneiras pelas quais este teorema enriquece nossas vidas.
Key Questions Answered
Como o Teorema de Pitágoras é usado em engenharia?
O Teorema de Pitágoras é usado em engenharia para calcular comprimentos, áreas e volumes de estruturas e componentes.
Quais são algumas aplicações do Teorema de Pitágoras na arquitetura?
O Teorema de Pitágoras é usado em arquitetura para calcular alturas de edifícios, áreas de salas e comprimentos de telhados.
Como posso usar o Teorema de Pitágoras para resolver problemas do mundo real?
Você pode usar o Teorema de Pitágoras para resolver problemas envolvendo distâncias, alturas e áreas, como calcular a altura de uma árvore ou a distância entre dois pontos.

