Relações Trigonométricas No Triângulo Retângulo Exemplos oferece uma introdução profunda ao estudo das relações trigonométricas, explorando seus conceitos fundamentais e aplicações práticas. O triângulo retângulo, com seus elementos característicos – hipotenusa, cateto adjacente e cateto oposto – serve como base para a definição das seis relações trigonométricas: seno, cosseno, tangente, cotangente, secante e cossecante.
Essas relações são expressas como razões entre os lados do triângulo retângulo, fornecendo uma ferramenta poderosa para calcular medidas de ângulos e lados, encontrando aplicações em diversas áreas, como engenharia, arquitetura e navegação.
Este estudo aprofunda a compreensão das relações trigonométricas, explorando sua relação com o círculo trigonométrico. Através do círculo trigonométrico, podemos visualizar as relações trigonométricas como coordenadas de pontos, expandindo seu escopo para além do triângulo retângulo e abrindo portas para uma análise mais abrangente de funções trigonométricas.
Introdução às Relações Trigonométricas no Triângulo Retângulo: Relações Trigonométricas No Triângulo Retângulo Exemplos

O estudo das relações trigonométricas no triângulo retângulo é fundamental para a compreensão de diversos campos da matemática, física e engenharia. O triângulo retângulo, como o próprio nome sugere, possui um ângulo reto (90°), e é a base para a definição das funções trigonométricas.
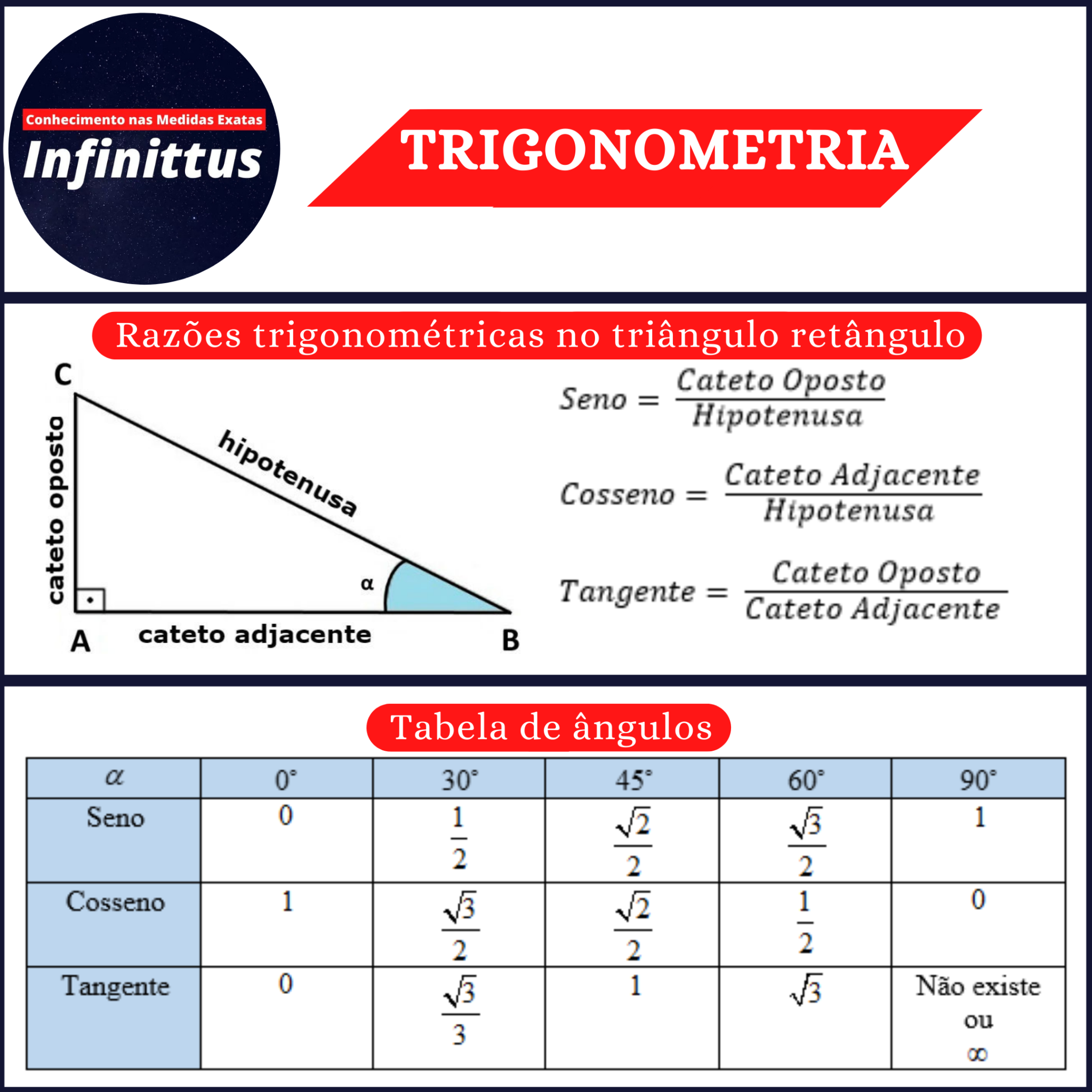
Elementos do Triângulo Retângulo
O triângulo retângulo possui três lados:
- Hipotenusa:O lado oposto ao ângulo reto, sendo o maior lado do triângulo.
- Catetos:Os dois lados que formam o ângulo reto. Um cateto é chamado de adjacenteem relação a um ângulo agudo, se ele é um dos lados que formam o ângulo. O outro cateto é chamado de opostoem relação ao mesmo ângulo.
Definição das Relações Trigonométricas
As seis relações trigonométricas básicas são definidas como razões entre os lados do triângulo retângulo em relação a um ângulo agudo:
- Seno (sen):A razão entre o cateto oposto e a hipotenusa.
- Cosseno (cos):A razão entre o cateto adjacente e a hipotenusa.
- Tangente (tg):A razão entre o cateto oposto e o cateto adjacente.
- Cotangente (cotg):A razão entre o cateto adjacente e o cateto oposto. É o inverso da tangente.
- Secante (sec):A razão entre a hipotenusa e o cateto adjacente. É o inverso do cosseno.
- Cossecante (csc):A razão entre a hipotenusa e o cateto oposto. É o inverso do seno.
Relações Trigonométricas e Razões entre os Lados
As relações trigonométricas podem ser representadas como razões entre os lados do triângulo retângulo.
sen θ = cateto oposto / hipotenusacos θ = cateto adjacente / hipotenusatg θ = cateto oposto / cateto adjacentecotg θ = cateto adjacente / cateto opostosec θ = hipotenusa / cateto adjacentecsc θ = hipotenusa / cateto oposto
Aplicações das Relações Trigonométricas
As relações trigonométricas, seno, cosseno e tangente, são ferramentas poderosas que permitem calcular medidas de ângulos e lados de triângulos retângulos. Essas relações são amplamente aplicadas em diversas áreas do conhecimento, como engenharia, arquitetura, navegação e física, entre outras.
Aplicações Práticas das Relações Trigonométricas
As relações trigonométricas são ferramentas essenciais para resolver problemas que envolvem triângulos retângulos, encontrando medidas de ângulos e lados desconhecidos. A seguir, são apresentados exemplos de como essas relações são utilizadas em diferentes áreas:
- Engenharia:Na construção de pontes, edifícios e outras estruturas, as relações trigonométricas são utilizadas para calcular ângulos de inclinação, comprimentos de vigas e outras medidas essenciais para garantir a segurança e estabilidade da estrutura.
- Arquitetura:Arquitetos utilizam as relações trigonométricas para projetar telhados, rampas e outros elementos arquitetônicos, garantindo que as medidas sejam precisas e que os ângulos sejam adequados para a funcionalidade e estética da estrutura.
- Navegação:Na navegação marítima e aérea, as relações trigonométricas são usadas para determinar a posição de um navio ou avião em relação a um ponto de referência, calcular a distância percorrida e a direção a seguir.
- Física:As relações trigonométricas são aplicadas em diversos campos da física, como a mecânica, a óptica e a eletricidade, para calcular vetores, forças e outros parâmetros físicos.
Exemplo de Problema: Cálculo da Altura de um Prédio
Imagine que você precisa determinar a altura de um prédio. Você sabe que a distância entre você e o prédio é de 50 metros e que o ângulo de elevação do topo do prédio em relação ao seu ponto de observação é de 30 graus.
Para calcular a altura do prédio, podemos utilizar a tangente do ângulo de elevação:
tan(30°) = altura do prédio / distância entre você e o prédio
Sabemos que tan(30°) = 1/√
Substituindo os valores na equação, temos:
/√3 = altura do prédio / 50 metros
Resolvendo a equação para a altura do prédio, obtemos:
altura do prédio = 50 metros / √3 ≈ 28,87 metros
Portanto, a altura do prédio é aproximadamente 28,87 metros.
Relações Trigonométricas e o Círculo Trigonométrico
O círculo trigonométrico é uma ferramenta fundamental para visualizar e compreender as relações trigonométricas. Ele fornece um contexto geométrico para as funções seno, cosseno e tangente, além de permitir a análise de ângulos maiores que 90 graus.
Relação entre as Relações Trigonométricas e o Círculo Trigonométrico
O círculo trigonométrico é um círculo com raio 1, centrado na origem de um sistema de coordenadas cartesianas. Cada ponto no círculo pode ser representado pelas coordenadas (x, y), onde x é a coordenada horizontal (cosseno) e y é a coordenada vertical (seno) do ângulo correspondente.
As relações trigonométricas são definidas como razões entre os lados de um triângulo retângulo, e no círculo trigonométrico, essas razões são interpretadas como as coordenadas do ponto no círculo.
A relação entre as relações trigonométricas e o círculo trigonométrico reside na conexão entre o ângulo e as coordenadas do ponto no círculo. Para um ângulo θ, o ponto no círculo com coordenadas (cos θ, sen θ) representa a projeção do ponto no eixo x (cosseno) e no eixo y (seno).
Determinando as Coordenadas de um Ponto no Círculo Trigonométrico
As relações trigonométricas podem ser utilizadas para determinar as coordenadas de um ponto no círculo trigonométrico, dado o ângulo.
Cálculo das Coordenadas
Seno
A coordenada y do ponto no círculo trigonométrico é igual ao seno do ângulo.
Cosseno
A coordenada x do ponto no círculo trigonométrico é igual ao cosseno do ângulo.
Tangente
A tangente do ângulo é a razão entre o seno e o cosseno, ou seja, y/x.
Exemplo
Considere o ângulo de 30 graus. O seno de 30 graus é 1/2, e o cosseno de 30 graus é √3/2. Portanto, as coordenadas do ponto no círculo trigonométrico correspondente a 30 graus são (√3/2, 1/2).
Valores das Relações Trigonométricas para Diferentes Ângulos
O círculo trigonométrico é dividido em quatro quadrantes, cada um com valores específicos para as relações trigonométricas.
Quadrante I (0° a 90°)
Seno
Positivo
Cosseno
Positivo
Tangente
Positiva
Quadrante II (90° a 180°)
Seno
Positivo
Cosseno
Negativo
Tangente
Negativa
Quadrante III (180° a 270°)
Seno
Negativo
Cosseno
Negativo
Tangente
Positiva
Quadrante IV (270° a 360°)
Seno
Negativo
Cosseno
Positivo
Tangente
Negativa
Gráfico do Círculo Trigonométrico
[Aqui seria inserido um gráfico do círculo trigonométrico com os valores das relações trigonométricas para diferentes ângulos. A descrição do gráfico seria detalhada, incluindo os pontos importantes, os valores das relações trigonométricas em cada quadrante e a relação entre o ângulo e as coordenadas.]A exploração das relações trigonométricas no triângulo retângulo, com exemplos práticos e sua conexão com o círculo trigonométrico, revela a riqueza e a versatilidade dessa área da matemática. O conhecimento das relações trigonométricas é fundamental para a resolução de problemas em diversas áreas, desde a construção de edifícios até a navegação marítima.
Através do estudo aprofundado dessas relações, podemos compreender melhor o mundo que nos cerca e desenvolver soluções inovadoras para os desafios da nossa época.

